ಗೇರ್‌ಗಳಲ್ಲಿ ವೃತ್ತಾಕಾರದ ಪಿಚ್ ಎಂದರೇನು?

ಗೇರ್ ಎಂಜಿನಿಯರಿಂಗ್‌ನಲ್ಲಿ,ವೃತ್ತಾಕಾರದ ಪಿಚ್ಗೇರ್ ಸುತ್ತಲಿನ ಹಲ್ಲುಗಳ ಅಂತರವನ್ನು ವಿವರಿಸಲು ಬಳಸುವ ಅತ್ಯಂತ ಮೂಲಭೂತ ಅಳತೆಗಳಲ್ಲಿ ಒಂದಾಗಿದೆ. ಇದು ಗೇರ್‌ಗಳು ಹೇಗೆ ಮೆಶ್ ಆಗುತ್ತವೆ, ಚಲನೆಯನ್ನು ರವಾನಿಸುತ್ತವೆ ಮತ್ತು ವಿದ್ಯುತ್ ಪ್ರಸರಣ ವ್ಯವಸ್ಥೆಗಳಲ್ಲಿ ಸಿಂಕ್ರೊನೈಸೇಶನ್ ಅನ್ನು ಹೇಗೆ ನಿರ್ವಹಿಸುತ್ತವೆ ಎಂಬುದರ ಮೇಲೆ ನೇರವಾಗಿ ಪರಿಣಾಮ ಬೀರುತ್ತದೆ. ನಿಖರವಾದ ಗೇರ್ ವಿನ್ಯಾಸ ಮತ್ತು ಸಂಯೋಗದ ಗೇರ್‌ಗಳ ನಡುವಿನ ಹೊಂದಾಣಿಕೆಗೆ ವೃತ್ತಾಕಾರದ ಪಿಚ್ ಅನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳುವುದು ಅತ್ಯಗತ್ಯ.

ವೃತ್ತಾಕಾರದ ಪಿಚ್‌ನ ವ್ಯಾಖ್ಯಾನ

ವೃತ್ತಾಕಾರದ ಪಿಚ್ (p) ಅನ್ನು ಒಂದು ಗೇರ್ ಹಲ್ಲಿನ ಮೇಲಿನ ಬಿಂದುವಿನಿಂದ ಮುಂದಿನ ಹಲ್ಲಿನ ಮೇಲಿನ ಅನುಗುಣವಾದ ಬಿಂದುವಿನ ನಡುವಿನ ಅಂತರ ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ, ಇದನ್ನು ಪಿಚ್ ವೃತ್ತದ ಉದ್ದಕ್ಕೂ ಅಳೆಯಲಾಗುತ್ತದೆ.
ದಿಪಿಚ್ ಸರ್ಕಲ್ಸ್ವತಃ ಒಂದು ಕಾಲ್ಪನಿಕ ಉಲ್ಲೇಖ ವೃತ್ತವಾಗಿದ್ದು ಅದು ಎರಡು ಸಂಯೋಗದ ಗೇರ್‌ಗಳ ನಡುವಿನ ಸಂಪರ್ಕ ಬಿಂದುವನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ.

ಎರಡು ಗೇರ್‌ಗಳು ಸರಿಯಾಗಿ ಮೆಶ್ ಆಗಬೇಕಾದರೆ, ಅವುಗಳ ವೃತ್ತಾಕಾರದ ಪಿಚ್‌ಗಳು ಸಮಾನವಾಗಿರಬೇಕು, ಒಂದು ಗೇರ್‌ನಲ್ಲಿರುವ ಪ್ರತಿಯೊಂದು ಹಲ್ಲು ಇನ್ನೊಂದರ ಹಲ್ಲುಗಳ ನಡುವಿನ ಜಾಗಕ್ಕೆ ಸಂಪೂರ್ಣವಾಗಿ ಹೊಂದಿಕೊಳ್ಳುತ್ತದೆ ಎಂದು ಖಚಿತಪಡಿಸಿಕೊಳ್ಳಬೇಕು.

ಸೂತ್ರ ಮತ್ತು ಲೆಕ್ಕಾಚಾರ

ವೃತ್ತಾಕಾರದ ಪಿಚ್ ಅನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವ ಸೂತ್ರವನ್ನು ಪಿಚ್ ವೃತ್ತದ ಸುತ್ತಳತೆ ಮತ್ತು ಹಲ್ಲುಗಳ ಸಂಖ್ಯೆಯಿಂದ ಪಡೆಯಲಾಗಿದೆ: p=πd​/N

ಎಲ್ಲಿ:

•  p = ವೃತ್ತಾಕಾರದ ಪಿಚ್

• d = ಪಿಚ್ ವ್ಯಾಸ (ಪಿಚ್ ವೃತ್ತದ ವ್ಯಾಸ)

• N = ಹಲ್ಲುಗಳ ಸಂಖ್ಯೆ

ಈ ಸೂತ್ರವು ವೃತ್ತಾಕಾರದ ಪಿಚ್ ಗೇರ್‌ನ ಗಾತ್ರ ಮತ್ತು ಅದರ ಹಲ್ಲುಗಳ ಸಂಖ್ಯೆಯನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ ಎಂದು ತೋರಿಸುತ್ತದೆ - ದೊಡ್ಡ ಗೇರ್‌ಗಳು ಅಥವಾ ಕಡಿಮೆ ಹಲ್ಲುಗಳು ದೊಡ್ಡ ಪಿಚ್ ಅಂತರಕ್ಕೆ ಕಾರಣವಾಗುತ್ತವೆ.

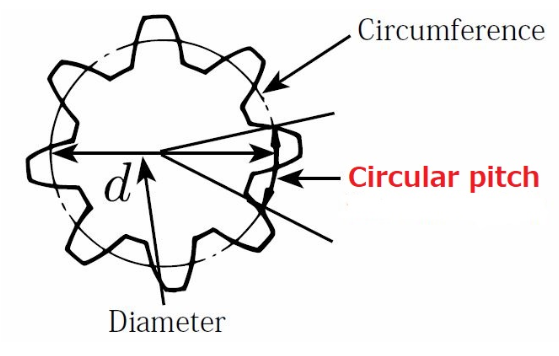
ವೃತ್ತಾಕಾರದ ಪಿಚ್ ಮತ್ತು ವ್ಯಾಸದ ಪಿಚ್ ನಡುವಿನ ಸಂಬಂಧ

ವೃತ್ತಾಕಾರದ ಪಿಚ್, ಸಾಮ್ರಾಜ್ಯಶಾಹಿ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ವ್ಯಾಪಕವಾಗಿ ಬಳಸಲಾಗುವ ವ್ಯಾಸ ಪಿಚ್ (P) ಎಂದು ಕರೆಯಲ್ಪಡುವ ಮತ್ತೊಂದು ಸಾಮಾನ್ಯ ಗೇರ್ ಮಾಪನಕ್ಕೆ ನಿಕಟ ಸಂಬಂಧ ಹೊಂದಿದೆ.

ವ್ಯಾಸದ ಪಿಚ್ ಪಿಚ್ ವ್ಯಾಸದ ಪ್ರತಿ ಇಂಚಿನ ಹಲ್ಲುಗಳ ಸಂಖ್ಯೆಯನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ ಮತ್ತು ಎರಡನ್ನೂ ಗಣಿತೀಯವಾಗಿ ಈ ಕೆಳಗಿನಂತೆ ಸಂಪರ್ಕಿಸಲಾಗಿದೆ: p=π​/p

ಈ ಸಂಬಂಧವು ಎಂಜಿನಿಯರ್‌ಗಳು ಮೆಟ್ರಿಕ್-ಆಧಾರಿತ (ವೃತ್ತಾಕಾರದ ಪಿಚ್) ಮತ್ತು ಸಾಮ್ರಾಜ್ಯಶಾಹಿ-ಆಧಾರಿತ (ವ್ಯಾಸದ ಪಿಚ್) ಗೇರ್ ವ್ಯವಸ್ಥೆಗಳ ನಡುವೆ ಸುಲಭವಾಗಿ ಪರಿವರ್ತಿಸಲು ಅನುವು ಮಾಡಿಕೊಡುತ್ತದೆ.

ವೃತ್ತಾಕಾರದ ಪಿಚ್ ಅನ್ನು ಯಾವಾಗ ಬಳಸಬೇಕು

ಅನೇಕ ಸಾಮಾನ್ಯ ಗೇರ್ ಅನ್ವಯಿಕೆಗಳಲ್ಲಿ ವ್ಯಾಸದ ಪಿಚ್ ಪ್ರಮಾಣಿತವಾಗಿದ್ದರೂ, ವೃತ್ತಾಕಾರದ ಪಿಚ್ ನಿರ್ದಿಷ್ಟ ಸಂದರ್ಭಗಳಲ್ಲಿ ಪ್ರಯೋಜನಗಳನ್ನು ನೀಡುತ್ತದೆ:

1. ಲೀನಿಯರ್ ಮೋಷನ್ ಸಿಸ್ಟಮ್ಸ್ (ರ್ಯಾಕ್ ಮತ್ತು ಪಿನಿಯನ್):
ವೃತ್ತಾಕಾರದ ಪಿಚ್ ರ್ಯಾಕ್ ಮತ್ತು ಪಿನಿಯನ್ ವ್ಯವಸ್ಥೆಗಳಿಗೆ ಸೂಕ್ತವಾಗಿದೆ, ಅಲ್ಲಿ ತಿರುಗುವಿಕೆಯ ಚಲನೆಯನ್ನು ರೇಖೀಯ ಚಲನೆಯಾಗಿ ಪರಿವರ್ತಿಸಲಾಗುತ್ತದೆ. ವೃತ್ತಾಕಾರದ ಪಿಚ್ ಅನ್ನು ಬಳಸುವುದರಿಂದ ಸೂಚ್ಯಂಕ ಮತ್ತು ಸ್ಥಾನೀಕರಣವನ್ನು ಸರಳಗೊಳಿಸುತ್ತದೆ, ಏಕೆಂದರೆ ಪ್ರತಿ ತಿರುಗುವಿಕೆಯು ಸ್ಥಿರ ರೇಖೀಯ ದೂರಕ್ಕೆ ಅನುಗುಣವಾಗಿರುತ್ತದೆ.
2. ದೊಡ್ಡ ವ್ಯಾಸದ ಗೇರುಗಳು:
ದೊಡ್ಡ ಗೇರ್‌ಗಳಿಗೆ, ವೃತ್ತಾಕಾರದ ಪಿಚ್ ಹಲ್ಲಿನ ಅಂತರದ ನೇರ ಅಳತೆಯನ್ನು ಒದಗಿಸುತ್ತದೆ, ಇದು ವ್ಯಾಸದ ಪಿಚ್‌ಗಿಂತ ಹೆಚ್ಚು ಅರ್ಥಗರ್ಭಿತ ಮತ್ತು ಅರ್ಥೈಸಲು ಸುಲಭವಾಗುತ್ತದೆ.
3. ಮೆಟ್ರಿಕ್ ಆಧಾರಿತ ವಿನ್ಯಾಸಗಳು:
ಮೆಟ್ರಿಕ್ ಎಂಜಿನಿಯರಿಂಗ್ ವ್ಯವಸ್ಥೆಗಳಲ್ಲಿ, ವೃತ್ತಾಕಾರದ ಪಿಚ್ ಅಳತೆಯ ಆದ್ಯತೆಯ ಘಟಕವಾಗಿದ್ದು, ಗೇರ್ ಗಾತ್ರ ಮತ್ತು ಲೆಕ್ಕಾಚಾರಗಳಲ್ಲಿ ಸ್ಥಿರತೆಯನ್ನು ಒದಗಿಸುತ್ತದೆ.

ವೃತ್ತಾಕಾರದ ಪಿಚ್ ಗೇರ್ ಜ್ಯಾಮಿತಿಯಲ್ಲಿ ಪ್ರಮುಖ ನಿಯತಾಂಕವಾಗಿದ್ದು, ಹಲ್ಲುಗಳು ಹೇಗೆ ಅಂತರದಲ್ಲಿರುತ್ತವೆ ಮತ್ತು ಎರಡು ಗೇರ್‌ಗಳು ಎಷ್ಟು ಸರಾಗವಾಗಿ ಮೆಶ್ ಆಗುತ್ತವೆ ಎಂಬುದನ್ನು ನಿರ್ಧರಿಸುತ್ತದೆ. ಈ ಅಳತೆಯ ನಿಖರವಾದ ನಿಯಂತ್ರಣವು ಯಾಂತ್ರಿಕ ವ್ಯವಸ್ಥೆಗಳಲ್ಲಿ ಪರಿಣಾಮಕಾರಿ ಚಲನೆಯ ವರ್ಗಾವಣೆ, ಕನಿಷ್ಠ ಉಡುಗೆ ಮತ್ತು ವಿಶ್ವಾಸಾರ್ಹ ಕಾರ್ಯಕ್ಷಮತೆಯನ್ನು ಖಚಿತಪಡಿಸುತ್ತದೆ.

ಬೆಲೋನ್ ಗೇರ್‌ನಲ್ಲಿ, ನಾವು ಆಪ್ಟಿಮೈಸ್ಡ್ ಟೂತ್ ರೇಖಾಗಣಿತದೊಂದಿಗೆ ಹೆಚ್ಚಿನ ನಿಖರತೆಯ ಗೇರ್‌ಗಳನ್ನು ತಯಾರಿಸುವಲ್ಲಿ ಪರಿಣತಿ ಹೊಂದಿದ್ದೇವೆ - ಸ್ಥಿರವಾದ ವೃತ್ತಾಕಾರದ ಪಿಚ್ ಮತ್ತು ದೋಷರಹಿತ ಮೆಶಿಂಗ್ ಕಾರ್ಯಕ್ಷಮತೆಯನ್ನು ಖಚಿತಪಡಿಸಿಕೊಳ್ಳುತ್ತೇವೆ.ಆಟೋಮೋಟಿವ್, ರೊಬೊಟಿಕ್ಸ್, ಮತ್ತು ಕೈಗಾರಿಕಾ ಯಂತ್ರೋಪಕರಣಗಳು.